前提
統計力学=マクロな系の平衡状態をマクロな性質を、系のミクロな力学の情報に基づいて、定量的に特徴づける理論
熱力学における平衡状態の普遍性=どのような環境で平衡状態を用意しても全く同じ平衡状態が得られる。
平衡状態を$(T; V, N)$と記述する。
カノニカルアンサンブル(以下、CE)で想定する状況は以下の図に示す通り。
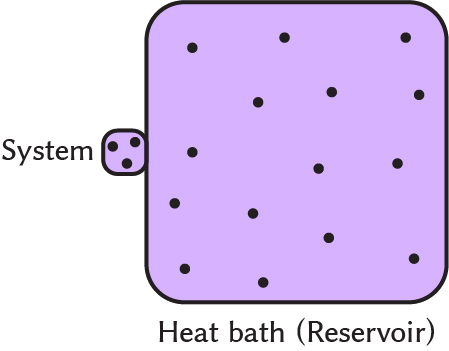
マクロな量子系のエネルギー固有状態を$i = 1, 2, \cdots , n$と番号付けし、対応するエネルギー固有値を$E_i$とおく。
熱浴を1種類の粒子からなる系とする。 熱浴の体積を$V_\mathrm{R}$、粒子数を$N_\mathrm{R}$とし、エネルギー固有状態を$k=1, 2, \cdots$、エネルギー固有値を$B_i$とする。
注目する系と熱浴を合わせた全系の量子状態は$(i, k)$で指定され、系と熱浴の間に相互作用が無視できるほどに小さいならば、$(i, k)$が全系のエネルギー固有状態を指定し、対応するエネルギー固有値は$E_i + B_k$となる。
Canonical Ensembleの導出
全系(注目する系+熱浴)が平衡状態にあるとする。 マクロに見た全系のエネルギーを$U_\mathrm{tot}$とする。
この平衡状態において、注目する系と熱浴の間の相互作用は無視できるほど小さいとする。
まず、全系の平衡状態をミクロカノニカルアンサンブルで記述する。 つまり、
$$ U_\mathrm{tot} - (V_\mathrm{R}+V)\delta < E_i + B_i \leq U_\mathrm{tot}, $$
を満たす$(i, k)$が「許されるエネルギー固有状態」であり、これらが等確率で出現するモデルを考える。 実際には、熱浴の体積が注目する系の体積よりも十分に大きいので、
$$ U_\mathrm{tot} - V_\mathrm{R}\delta < E_i + B_i \leq U_\mathrm{tot}, $$
とできる。
注目する系のエネルギ固有値$i=1, 2,\cdots,n$を1つ固定すると、熱浴のエネルギー固有状態$k=1, 2, \cdots$として「許される」のは、
$$ U_\mathrm{tot} - E_i - V_\mathrm{R}\delta < B_i \leq U_\mathrm{tot} - E_i, $$
を満たすものである。 これを満たす$k$の総数は、熱浴の状態数を使って、
$$ \Omega_i = N_\mathrm{R}!\Omega_\mathrm{R}(U_\mathrm{tot}-E_i) - N_\mathrm{R}!\Omega_\mathrm{R}(U_\mathrm{tot}-E_i- V_\mathrm{R}\delta), $$
と記述できる。 これを$i$について足し合わせたものが全系に「許されたエネルギー固有状態」の総数で、
$$ \Omega_\mathrm{total} := \sum^n_{i=1}\Omega_i. $$
今想定しているモデルでは、この$\Omega_\mathrm{total}$個の状態が等確率$1/\Omega_\mathrm{total}$で出現することを考える。 また、注目する系が固有状態$i$をとる確率$p_i$は、
$$ p_i = \frac{\Omega_i}{\Omega_\mathrm{total}}, $$
となる。
仮定により、熱浴の状態数$\Omega_\mathrm{R}(B)$は、ある関数$\sigma(u, \rho)$を用いて、
$$ \begin{align} \Omega_\mathrm{R}(B) &= \exp[V_\mathrm{R}\sigma(B/V_\mathrm{R}, N_\mathrm{R}/V_\mathrm{R})+o(V_\mathrm{R})]. \end{align} $$
ここで、$\tilde{U} = U_\mathrm{tot}-E_i$から、
$$ \begin{aligned} \frac{\Omega_\mathrm{R}(\tilde{U}-V_\mathrm{R}\delta)}{\Omega_\mathrm{R}(\tilde{U})} &= \exp[V_\mathrm{R}{\sigma(\tilde{t} - \delta, \rho) - \sigma(\tilde{u}, \rho)} + o(V_\mathrm{R})]\ &= \exp[V_\mathrm{R}\left(\frac{\partial}{\partial \tilde{u}}\sigma(\tilde{u, \rho})\delta + O(\delta^2)\right)+o(V_\mathrm{R})] \ll 1, \end{aligned} $$
を満たす。ここで、$\tilde{u} = \tilde{U}/V_\mathrm{R}, \rho=N_\mathrm{R}/V_\mathrm{R}$とした。 また、$\partial\sigma(\tilde{u, \rho})/\partial \tilde{u}>0$と$\delta>0$が熱浴の体積$V_\mathrm{R}$に依存せず、$V_\mathrm{R}$は十分に大きいとした。
次に、$p_i$を以下の様に書き直す。
$$ p_i \simeq \frac{N_\mathrm{R}!\Omega_\mathrm{R}(U_\mathrm{tot}-E_i)}{\sum^n_{j=1}N_\mathrm{R}!\Omega_\mathrm{R}(U_\mathrm{tot}-E_j)}=\frac{\Omega_\mathrm{R}(U_\mathrm{tot}-E_i)}{\Omega_\mathrm{R}(U_\mathrm{tot})}\left(\sum^n_{j=1}\frac{\Omega_\mathrm{R}(U_\mathrm{tot}-E_j)}{\Omega_\mathrm{R}(U_\mathrm{tot})} \right)^{-1}. $$
この中の括弧外について、対数を取ってTaylor展開すると、
$$ \ln \frac{\Omega_\mathrm{R}(U_\mathrm{tot}-E_i)}{\Omega_\mathrm{R}(U_\mathrm{tot})} = \ln \Omega_\mathrm{R}(U_\mathrm{tot}-E_i) - \ln\Omega_\mathrm{R}(U_\mathrm{tot})\ = -E_i \frac{\partial}{\partial U}\ln \Omega_\mathrm{R}(U)|{U=U\mathrm{tot}} - \frac{E_i^2}{2} \frac{\partial^2}{\partial U^2}\ln \Omega_\mathrm{R}(U)|{U=U\mathrm{tot}} + \cdots, $$
ここで、$\rho=N_\mathrm{R}/V_\mathrm{R}, u=U_\mathrm{tot}/V_\mathrm{R}$として、式(1)を用いて、
$$ =-\frac{E_i}{V_\mathrm{R}}\frac{\partial}{\partial u}\left{V_\mathrm{R}\sigma(u, \rho) + o(V_\mathrm{R})\right} + \frac{E_i^2}{2V_\mathrm{R}^2}\frac{\partial^2}{\partial u^2}(V_\mathrm{R}\sigma(u, \rho)+o(V_\mathrm{R}))+ \cdots\ = -E_i \frac{\partial}{\partial u}\sigma(u, \rho) + \frac{1}{V_\mathrm{R}}\frac{E_i^2}{2}\frac{\partial^2}{\partial u^2}\sigma(u, \rho) + \cdots + \frac{o(V_\mathrm{R})}{V_\mathrm{R}}. $$
すなわち、$V_\mathrm{R}$が十分に大きいなら、
$$ \ln \frac{\Omega_\mathrm{R}(U_\mathrm{tot}-E_i)}{\Omega_\mathrm{R}(U_\mathrm{tot})} \simeq -\beta(u, \rho)E_i. $$
あるいは、
$$ \begin{align} \frac{\Omega_\mathrm{R}(U_\mathrm{tot}-E_i)}{\Omega_\mathrm{R}(U_\mathrm{tot})} \simeq \exp(-\beta(u, \rho)E_i). \end{align} $$
ここで、
$$ \beta(u, \rho) := \frac{\partial}{\partial u}\sigma(u, \rho) = \frac{\partial}{\partial U}\ln \Omega_\mathrm{R}(U)|{U=U\mathrm{tot}} > 0. $$
式(2, 3)より、
$$ p_i^{(\mathrm{can}, \beta)} = \frac{\exp(-\beta E_i)}{Z(\beta)}, $$
が、$u$と$\rho$を一定にしながら全エネルギー$U_\mathrm{tot}$、熱浴の体積$V_\mathrm{R}$、熱浴の粒子数$N_\mathrm{R}$を大きくすれば等式として得られる。
この$Z(\beta)$は分配関数で、$Z(\beta):=\sum_i \exp(-\beta E_i)$となる規格化定数である。 また、$\exp(-\beta E_i)$はBoltzmann因子と呼ばれる。
メモ:状態数の振る舞い
田崎晴明「統計力学I」の3章より
外界から孤立した量子系に対して、全てのエネルギー固有状態を列挙し、全てのエネルギー固有値を求めることが出来たとする。 この時、この量子系の状態数$\Omega(E)$を、「エネルギーが$E$以下であるエネルギー固有状態の総数」と定義する。
留意点:ある程度の大きさを持った系では一般にエネルギー固有値の間隔は極めて小さい。 → マクロなエネルギースケールでは、状態数は滑らかに増加する関数に見える。
例 1次元の自由粒子1つの系
長さ$L$の区間に閉じ込められた1つの粒子の状態数を考える。
境界より外に出ない様にする力以外はかからない(=境界条件)粒子=自由粒子
波動関数$\varphi$について、境界条件は
$$ \varphi(0) = \varphi(L) = 0. $$
ここで、変位$x$と運動量$p$は、2つの演算子
$$ \hat{x} \rightarrow x,\hspace{20pt} \hat{p} \rightarrow \frac{\hbar}{i}\frac{\mathrm{d}}{\mathrm{d}x}, $$
となり(掛け算演算子と微分演算子)、これらは正準交換関係$[\hat{x}, \hat{p}]= i\hbar$を満たす。 すなわち、粒子のエネルギーに対応する演算子であるハミルトニアン$\hat{H}$は、
$$ \hat{H}=\frac{\hat{p}^2}{2m} \rightarrow -\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}, $$
という2階微分の演算子に対応する。これを用いるとシュレディンガー方程式は、
$$ -\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}\varphi(x) = E\varphi(x), $$
となる。 境界条件に留意すると、解は$\varphi(x) = A\sin(kx)$の形で書けるはずなので、$\int _0^L|\varphi(x)|^2\mathrm{d}x=1$になる様に係数を選べば、
$$ \varphi(x) = \sqrt{\frac{2}{L}}\sin({kx}). $$
ここで、境界条件$\varphi(L) = 0$から、
$$ \varphi(x) = \sqrt{\frac{2}{L}}\sin\left({\frac{n\pi}{L}x}\right)\hspace{30pt}(n\in\mathbf{Z}). $$
これを、シュレディンガー方程式に代入すると、
$$ E_n = \frac{\hbar^2k^2}{2m} = \frac{\pi^2\hbar^2}{2mL^2}n^2 := E_0n^2. $$
状態数$\Omega(E)$の定義から、
$$ \begin{aligned} \Omega(E) &= (E_n \leq Eを満たす正整数nの総数)\ &= (n^2 \leq E/E_0を満たす正整数nの総数)\ &= (n \leq \sqrt{E/E_0}を満たす正整数nの総数), \end{aligned} $$
すると、$\Omega(E)$は$\sqrt{E/E_0}$を超えない最大の整数である。よって、
$$ \sqrt{\frac{E}{E_0}} - 1 \leq \Omega(E) \leq \sqrt{\frac{E}{E_0}}. $$
もしも$E \gg E_0$なら、左辺の$-1$は無視できるので、
$$ \Omega(E) \simeq \sqrt{\frac{E}{E_0}} = \frac{2m}{\pi\hbar}L\sqrt{E}. $$
状態数は系の大きさに依存し、エネルギーに関する滑らかな滑らかな関数で書ける。
例 3次元の自由粒子$N$個の系
以下、$N$はアヴォガドロ定数のオーダーの非常に大きな値とする。 系の体積$V$も大きい値とする。
1つの粒子の位置情報が3つの変数$x, y, z$で指定されるので、系のエネルギー固有状態は$3N$個の整数の組$(n_\alpha^{(j)})_{\alpha=\mathbf{x, y, z}; j=1,\cdots,N}$で指定される。
ここで、全系のエネルギー固有値は、全粒子のエネルギー固有値を足し合わせた、
$$ E_{(n_\alpha^{(j)}){\alpha=\mathbf{x, y, z}; j=1,\cdots,N}}=E_0\sum{\alpha=\mathbf{x, y, z}}\sum_{j=1}^N(n^{(j)}_\alpha)^2, $$
となる。 これを用いて状態数は、
$$ \Omega(E) = \frac{1}{N!}\left(E_{(n_\alpha^{(j)}){\alpha=\mathbf{x, y, z}; j=1,\cdots,N}}\leq Eを満たす組(n\alpha^{(j)}){\alpha=\mathbf{x, y, z}; j=1,\cdots,N}の総数\right)\ = \frac{1}{N!}\left(\sum{\alpha=\mathbf{x, y, z}}\sum_{j=1}^N(n^{(j)}\alpha)^2\leq \frac{E}{E_0}を満たす組(n\alpha^{(j)})_{\alpha=\mathbf{x, y, z}; j=1,\cdots,N}の総数\right), $$
である。ここで、粒子の区別をしないために$N!$で割った。 また、上で数える状態数の条件から、半径$\sqrt{E/E_0}$の$3N$次元球の中に点$(n_\alpha^{(j)})_{\alpha=\mathbf{x, y, z}; j=1,\cdots,N}$が格納される状況を考えればいい。
任意の正定数$\nu$と実数$R$について、$V_\nu(R)$を半径$R$の$\nu$次元球の体積とすると、$\nu$が偶数の時、 $$ V_\nu(R) = \frac{\pi^{\nu/2}}{(\nu/2)!}R^\nu, $$
となる。 この記号を用いて、かつ$3N$次元空間には区別のできない$2^{3N}$個の象限があることに留意すると、
$$ \Omega(E) \sim \frac{1}{N!}\frac{1}{2^{3N}}V_{3N}\left(\sqrt{\frac{E}{E_0}}\right). $$
粒子数$N$は偶数だとして、体積の公式と$E_0$の定義から、
$$ \Omega(E) \sim \frac{1}{N!}\frac{1}{2^{3N}}\frac{\pi^{3N/2}}{(3N/2)!}\left(\frac{E}{E_0}\right)^{3N/2}\ = \frac{1}{N!}\frac{1}{(3N/2)!}\left(\left(\frac{m}{2\pi}\right)^{3/2}\frac{1}{\hbar^3}\right)^NE^{3N/2}V^N.\ = \frac{1}{N!}\frac{1}{(3N/2)!} \tilde{\alpha}^NE^{3N/2}V^N. $$
ここで、$V = L^3$、$\tilde{\alpha}={m/(2\pi)}^{3/2}\hbar^{-3}$とした。
さらに$N \gg 1$を仮定してStirlingの公式を用いて、
$$ \Omega(E) \sim \left(\frac{e}{N}\right)^N\left(\frac{e}{3N/2}\right)^{3N/2}\tilde{\alpha}^NE^{3N/2}V^N = \alpha^N\left(\frac{E}{V}\right)^{3N/2}\left(\frac{V}{N}\right)^{5N/2}. $$
ここで、$\alpha := e^{5/2}(2/3)^{3/2}\tilde{\alpha}$とした。 さらに対数をとると、
$$ \ln \Omega(E) \simeq N\ln \left[\alpha \left(\frac{E}{V}\right)^{3/2} \left(\frac{V}{N}\right)^{5/2} \right] = V{\rho\ln (\alpha \epsilon^{3/2}\rho^{15/2}) }. $$
ここで、$\epsilon := E/V$、$\rho := N/V$とした。これは、
$$ \Omega(E) \sim \exp[V\rho\ln(\alpha \epsilon^{3/2}\rho^{15/2})] = \exp[V\sigma(\epsilon, \rho)]. $$
この$\sigma$は、熱力学的なエントロピーの定数倍である。(田崎晴明「統計力学I」培風館の9章参照)
一般のマクロな系での状態数
考える量子系=一辺が$L$の立方体の中に$N$個の質量$m$の粒子がある系
各粒子間には、ポテンシャル$v(r)$で記述される等方的な力が働く。このポテンシャルは、近距離では強い斥力を、遠距離では弱い引力を示すようなものを想定する(実際にはこれに限らないはず。あくまで例として)。
粒子に$j = 1, 2, \cdots, N$と名前をつけ、粒子$j$の位置を$\mathbf{r}_j$、運動量を$\mathbf{p}_j$と書けば、古典力学的エネルギーは、
$$ E = \sum^N_{j=1}\frac{|\mathbf{p}j|^2}{2m} + \sum^n{i, j=1 (i>j)}v(|\mathbf{r_i}-\mathbf{r_j}|). $$
以下、厳密な結果を示すためにポテンシャル$v(r)$について以下の2つの(ゆるい)条件を課す。
- 長距離での振る舞い: ある定数$r_0 > 0$があり、$^\forall r \geq r_0$について、 $$ v(r) \leq 0 $$ が成り立つ。
- 安定性: ある定数$b >0$があり、任意の粒子数$N$と任意の粒子位置$\mathbf{r}i$について、 $$ \sum^N{i, j=1(i>j)}v(|\mathbf{r}_i - \mathbf{r}_j|) \geq -bN, $$ が成り立つ。
以上の時、状態数$\Omega_{V, N}(E)$について、以下の結果が顕密に示されている。
Them 3.1 マクロな系の基底エネルギーと状態数の振る舞い
体積$V$、粒子数$N$の系の基底エネルギーを$E_{\mathrm{GS}}(V, N)$とする。$^\forall\rho >0$について、$\rho = N/V$を一定に保って体積を大きくしたときの基底エネルギー密度の極限
$$ \epsilon_0(\rho) = \lim_{V \nearrow \infty}\frac{E_{\mathrm{GS}}(V, N)}{V} $$
が存在する。ただし、$\epsilon_0(\rho)=\infty$の可能性もある。
$\epsilon_0(\rho) < \infty$とする。$^\forall\rho>0$と$^\forall\epsilon>\epsilon_0$について、密度$\rho = N/V$とエネルギー密度$\epsilon = E/V$を一定に保って体積を大きくしたときの極限
$$ \sigma(\epsilon, \rho) := \lim_{V\nearrow \infty}\frac{1}{V}\ln\Omega_{V, N}(E) $$
が存在する。関数$\sigma(\epsilon, \rho)$は、$\epsilon$の増加関数であり、2つの変数$\rho, \epsilon$について上に凸である。
この結果から、
$$ \Omega_{V, N}(E) \sim \exp[V\sigma(\epsilon, \rho)], $$
と書ける。
参考文献
田崎晴明「統計力学I」培風館、2008年