Jax.numpy使いたいし力学系も解析したい
今のところ、Jax.numpyの速さを実感しつつもメカニズムは理解していない。
が、どうせJax.numpyを使う機会が増えるので、力学系解析もJax.numpyでできるようにする。
ライブラリは、Diffraxを用いる。
https://github.com/patrick-kidger/diffrax
ODEだけではなく、SDEも簡単に扱える。今回はODEだけ。 CDE(Controlled Differeitial Equation)も扱えるらしいが、これが何かはまだ分かっていない。
とりあえず、Duffing方程式の時間発展までを行ってコードを確認する。
$$ \begin{aligned} \dot{x} &= v,\ \dot{v} &= x - x^3 - ev + \gamma\cos(\omega t). \end{aligned} $$
importとソルバーに入れる関数は以下。
import jax.numpy as jnp
from diffrax import diffeqsolve, ODETerm, Dopri5, SaveAt, PIDController
def Duffing(t, X, args):
x, v = X
dx = v
dv = x - x**3 - args['e']*v + args['g']*jnp.cos(t)
return [dx, dv]
関数の引数は、scipyのodeintと同じで、時間 tと変数 Xとパラメータ argsとする。
パラメータの与え方はいくつか考えられるが、今回は辞書型で与えている。
次に、実際に時間発展させるコードを見る。
ARGS = {'e': 0.02, 'g': 0.0}
# systemの定義
term = ODETerm(Duffing)
# solverの選択 5th-prder runge-kutta
solver = Dopri5()
# step size controller
stepsize_controller = PIDController(rtol=1e-5, atol=1e-5)
# 時系列のサンプリング点の予約
saveat = SaveAt(t0=True, t1=True, ts=jnp.linspace(0, 100, 1000))
# initial point
Y0 = [1.0, 0.1]
sol = diffeqsolve(
term, solver, t0=0, t1=100, dt0=0.01, y0=Y0, args=ARGS,
stepsize_controller=stepsize_controller, saveat=saveat
)
特に説明をすることはなく、コメントを見れば理解できると思われる。
SaveAtは数値計算した時系列から点を取るので、計算外の範囲を指定すると怒られる。
計算範囲はdifferqsolveの引数にあるt0, t1で指定する。
dt0は、初め一回のstep sizeで、Noneを指定すれば自動で決めてくれる。
solが計算結果となる。以下、少し補足。
# sol.tsで時間点を得られる。
print(type(sol.ts))
# -> <class 'jaxlib.xla_extension.ArrayImpl'>
# sol.ysで変数の時間発展を得られる。今回は2変数あるので2行のリスト。
print(type(sol.ys), len(sol.ys))
# -> <class 'list'> 2
例えば、これを可視化するなら以下のような感じになる。
import matplotlib.pyplot as plt
import seaborn
fig, axes = plt.subplots(1, 2, figsize=(6, 3), dpi=144)
seaborn.set_style('darkgrid')
plt.subplots_adjust(wspace=0.4)
# as time-series data
axes[0].scatter(sol.ts, sol.ys[0], s=1, c='blueviolet', label='x')
axes[0].scatter(sol.ts, sol.ys[1], s=1, c='magenta', label='v')
axes[0].legend(ncol=2, frameon=False, loc='best', fontsize=10)
# phase diagram
axes[1].scatter(sol.ys[0], sol.ys[1], s=0.1, c='blueviolet')
axes[1].set_xlabel('x')
axes[1].set_ylabel('v')
plt.show()
seabornはなくてもいいが、好みで。これで可視化した図は以下。
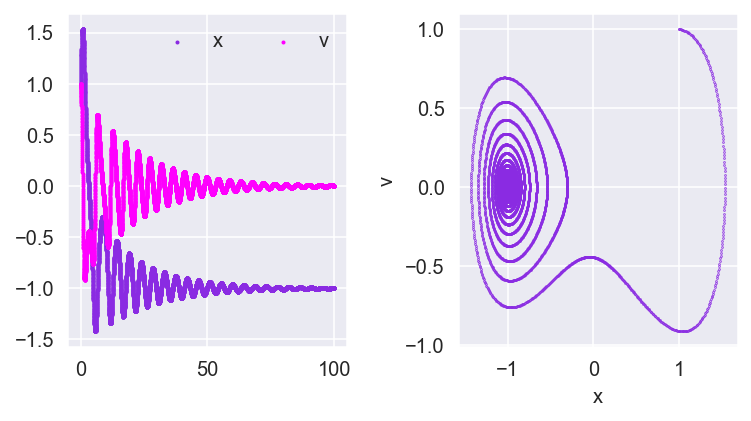
今回は係数$\gamma$を0にしたので、これを0.1にしたのも可視化したものを下に示す。カオスが見えるはず。
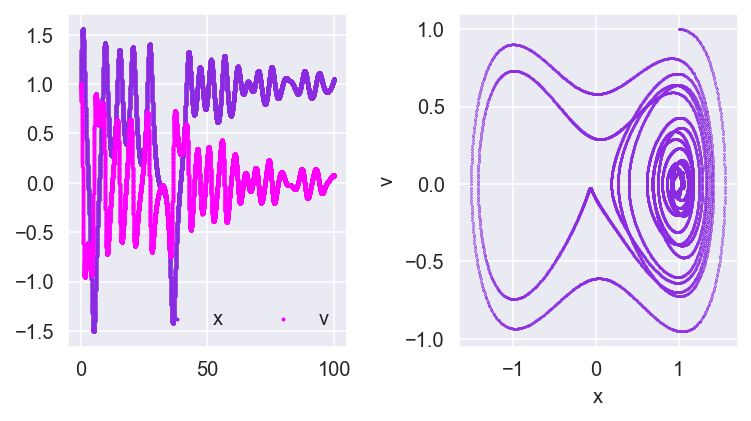
見えた。
ついでにヌルクラインを描く。
相図の描き方自体は、numpyを使う時と同じでjnp.meshgridとplt.contourを使う。
各変数単体の更新式を定義して、そこに点を代入して、0となる点の集団を可視化する、という流れ。
ARGS = {'e': 0.1, 'g': 0.0}
term = ODETerm(Duffing)
solver = Dopri5()
stepsize_controller = PIDController(rtol=1e-5, atol=1e-5)
saveat = SaveAt(t0=True, t1=True, ts=jnp.linspace(0, 100, 10000))
Y0 = [1.0, 1.0]
sol = diffeqsolve(
term, solver, t0=0, t1=100, dt0=0.1, y0=Y0, args=ARGS,
stepsize_controller=stepsize_controller, saveat=saveat
)
dxdt = lambda x, v, args: v
dvdt = lambda x, v, args: x - x**3 - args['e']*v
x, v = jnp.meshgrid(jnp.linspace(-2, 2, 100), jnp.linspace(-4.0, 4.0, 100))
dx = dxdt(x, v, ARGS)
dv = dvdt(x, v, ARGS)
fig, ax = plt.subplots(figsize=(3, 3), dpi=144)
seaborn.set_style('darkgrid')
ax.contour(x, v, dx, levels=0, colors='royalblue')
ax.contour(x, v, dv, levels=0, colors='magenta')
ax.scatter(sol.ys[0], sol.ys[1], s=0.1, c='k')
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
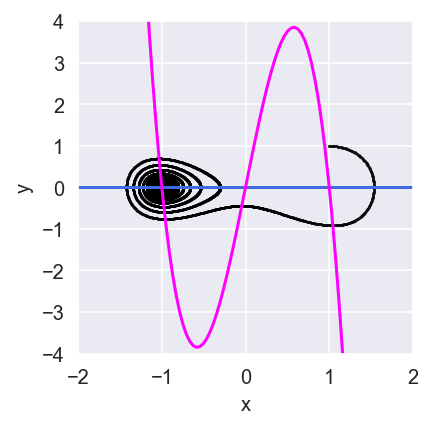
綺麗やね。